Buenas tardes a todos,
Ya había hablado antes sobre los conjuntos, pero con los conceptos nuevamente aprendidos, es bueno volverlos a plantear.
Empecemos otra vez por los naturales, aquellos números que nos sirven para contar: 1, 2, 3, 4,... y así hasta el infinito.
Bueno son muy buenos para contar cosas, como manzanas, o mejor no manzanas que siempre utilizamos manzanas, que tal kiwis, sí mejor kiwis.
Bueno, supongan que yo tengo 3 kiwis y me regalan otros 2 kiwis, entonces ahora tengo 3+2= 5 kiwis, vemos que 5 es otro número natural, por lo que podemos sumar con los naturales.
Ahora supongamos que estoy cumpliendo años, y todos mis amigos, unos 4, cada uno me regala 3 kiwis, entonces ahora tendre 3+3+3+3=4*3= 12 kiwis (ya me había comido los otros 5). Como vemos también podemos multiplicar en los naturales y da como resultado otro natural.
Propiedades:
La suma y la multiplicación son operaciones conmutativas, es decir que el orden en que se haga no importa el orden de los sumandos o de los factores, eso no afecta la suma o el producto.
También decimos que la suma es asociativa, pues si tenemos tres números naturales a, b y c
a+b+c=a+(b+c)=(a+b)+c
Tenemos las propiedades modulativas:
a+0 = a (suma)
a*1 = a (producto)
0 es el módulo para la suma y 1 para el producto.
Módulo es algo así como un número que al operar con él no altera el resultado. Este par de números nos serán muy útiles más adelante.
Finalmente tenemos las propiedades distributivas con respecto a la suma y al producto:
m*(a+b) = a*m+b*m
m*(a*b) = a*b*m
------------------------------o-------------------------------------
Sin embargo, sólo hemos visto un par de operaciones en los naturales, falta la resta o diferencia y la división, pues resulta que no podemos garantizar que estas dos operaciones nos den como resultado un número natural, por ejemplo: 2-3 o 11/5 dan como resultado números que no son naturales, qué podemos hacer, bueno nos ampliamos a un conjunto en el que podamos hacer estas operaciones.
Vamos por partes, primero la resta, entonces nos metemos al conjunto de los enteros, el cual incluye a los naturales (conocidos como enteros positivos) además del 0 y los enteros negativos (-1, -2, -3,...).
Ahora sí podemos hacer la resta que queramos sin salirnos del conjunto.
Ampliamos la propiedad conmutativa para incluir la resta, así, podemos definir una resta de la siguiente forma:
a-b=a+(-b)=(-b)+a
-b no es más que el inverso aditivo de b.
Como vemos la resta ahora queda dentro de nuestras propiedades.
Ahora, qué hacer con la división, bueno nos ampliamos al conjunto de los racionales.
El cual es el conjunto de números que se pueden expresar como razón de dos enteros: 1/2, -1/3, 5/25, etc.
También podemos expresar estos números en notación decimal: 0,5, -0,333..., etc.
Hay algunos racionales que son decimales periódicos, es decir que tienen algunas cifras decimales que se repiten infinitamente, como 0,333... y otros más complicados 1,4237585858... estos son racionales también.
Es decir son racionales todos los decimales finitos o periódicos.
A los racionales les sumamos un conjunto que nos hace falta para completar a los reales:
Los irraciionales, que son aquellos que se expresan como decimales con infinitas cifras decimales las cuales no se repiten. Son ejemplos de estos números: pi, e (Euler), raíz cuadrada de 2 y en general cualquier raíz cuadrada de un número primo.
M&M: Matemática & Música
viernes, 4 de febrero de 2011
jueves, 3 de febrero de 2011
Geometría vectorial 3: Matrices
Sobre las matrices simplemente son espacios vectoriales de mxn componentes.
En este caso los componentes (que también son números) están ordenados en filas y columnas. Una matriz de mxn tiene m filas y n columnas.
A los componentes de una matriz también se les conoce como entradas.
Las definiciones de igualdad, suma y producto por un escalar para las matrices son similares a las dadas para vectores.
Hay una definición más que es el de un producto entre dos matrices, pero de esta hablaré en una entrada posterior.
En este caso los componentes (que también son números) están ordenados en filas y columnas. Una matriz de mxn tiene m filas y n columnas.
A los componentes de una matriz también se les conoce como entradas.
Las definiciones de igualdad, suma y producto por un escalar para las matrices son similares a las dadas para vectores.
Hay una definición más que es el de un producto entre dos matrices, pero de esta hablaré en una entrada posterior.
Geometría vectorial 2: Más sobre espacios vectoriales y vectores
Una palabra más sobre espacios vectoriales o vectores.
Según el libro de Álgebra lineal de Grossman:
"Definimos un vector renglón de n componentes (o n-dimensional) como un conjunto ordenado de n números escrito como
(x1, x2, ... , xn)
Se puede dar una definición similar para un vector columna.
x1 (x sub 1, no sé como poner subíndices acá) es la primera componente del vector, x2 la segunda y así sucesivamente.
La palabra "ordenado" es muy importante, no es lo mismo el vector (0, 1) que el vector (1, 0).
Definimos que dos vectores A, B ambos miembros del mismo plano vectorial, es decir que ambos tienen el mismo número (n) de componentes, son iguales, si y sólo si cada uno de sus componentes correspondientes son iguales: A=B si y solo si a1 = b1, a2 = b2, ... , an = bn
Definimos la suma entre dos vectores A, B de nuevo ambos en el mismo plano vectorial (igual número de componentes) como la suma componente a componente de los dos vectores.
A+B = (a1+b1, a2+b2, ... , an+bn)
La suma da como resultado otro vector en el mismo campo vectorial (de igual número de componentes).
Es MUY IMPORTANTE que los dos vectores sean del mismo tamaño, si no es así la suma no está definida.
Definimos el vector O como el vector de n componentes todos los cuales son iguales a cero. También se le conoce como módulo de adición, pues A+O=A
El inverso aditivo de un vector A se nota con el signo -A y es igual a un vector cuyos elementos correspondientes tienen signo contrario. Se define como el vector tal que A+(-A)=0
Un detalle sobre la "diferencia" o "resta" de vectores: ya que dentro de un vector podemos tener números positivos o negativos, es mejor tratar una resta como la suma por el inverso aditivo (todos los componentes con signos cambiados) del otro vector para evitar tener confusiones con los signos.
La multiplicación de un vector por un escalar (en este caso un número real) es igual a otro vector en el que cada uno de sus elementos es igual al correspondiente el primer vector multiplicado por el escalar:
Sea A un vector en Rn es decir de n elementos ordenados y x un escalar.
xA = (x*a1, x*a2, ... , x*an)
No se define multiplicación entre vectores.
Según el libro de Álgebra lineal de Grossman:
"Definimos un vector renglón de n componentes (o n-dimensional) como un conjunto ordenado de n números escrito como
(x1, x2, ... , xn)
Se puede dar una definición similar para un vector columna.
x1 (x sub 1, no sé como poner subíndices acá) es la primera componente del vector, x2 la segunda y así sucesivamente.
La palabra "ordenado" es muy importante, no es lo mismo el vector (0, 1) que el vector (1, 0).
Definimos que dos vectores A, B ambos miembros del mismo plano vectorial, es decir que ambos tienen el mismo número (n) de componentes, son iguales, si y sólo si cada uno de sus componentes correspondientes son iguales: A=B si y solo si a1 = b1, a2 = b2, ... , an = bn
Definimos la suma entre dos vectores A, B de nuevo ambos en el mismo plano vectorial (igual número de componentes) como la suma componente a componente de los dos vectores.
A+B = (a1+b1, a2+b2, ... , an+bn)
La suma da como resultado otro vector en el mismo campo vectorial (de igual número de componentes).
Es MUY IMPORTANTE que los dos vectores sean del mismo tamaño, si no es así la suma no está definida.
Definimos el vector O como el vector de n componentes todos los cuales son iguales a cero. También se le conoce como módulo de adición, pues A+O=A
El inverso aditivo de un vector A se nota con el signo -A y es igual a un vector cuyos elementos correspondientes tienen signo contrario. Se define como el vector tal que A+(-A)=0
Un detalle sobre la "diferencia" o "resta" de vectores: ya que dentro de un vector podemos tener números positivos o negativos, es mejor tratar una resta como la suma por el inverso aditivo (todos los componentes con signos cambiados) del otro vector para evitar tener confusiones con los signos.
La multiplicación de un vector por un escalar (en este caso un número real) es igual a otro vector en el que cada uno de sus elementos es igual al correspondiente el primer vector multiplicado por el escalar:
Sea A un vector en Rn es decir de n elementos ordenados y x un escalar.
xA = (x*a1, x*a2, ... , x*an)
No se define multiplicación entre vectores.
martes, 1 de febrero de 2011
Geometría vectorial 1: Espacios vectoriales
Bueno, lo siento por esta entrada tan parca, pero simplemente quiero mencionar lo que vi hoy en mi primera clase del curso de Geometría Vectorial y Analítica: Espacios vectoriales.
Estos también son conocidos como conjuntos de n-tuplas, donde una n-tupla son varios elementos ordenados:
R^n = {(a_1, a_2,...,a_n)/tal que a_i está en R (conjunto de los reales), para todo i=1,...,n
Algunos de estos conjuntos son muy conocidos, por ejemplo el de las parejas ordenadas
R^2 = {(a_1,a_2)/a_1,a_2 en R}
Este tiene su representación como puntos en el plano cartesiano.
R^3 tiene su representación como puntos en un espacio tridimensional. Otros conjuntos R^n con n > 3 son también usados pero no tienen representación geométrica.
Recordemos que un elemento es una n-tupla (a_1,a_2,...,a_n), a su vez cada n-tupla tiene componentes que son a_1, a_2, etc. que para el curso son números reales).
Con los elementos de estos conjuntos podemos hacer algunas operaciones: la adición, el producto de un número real por una n-tupla y el producto escalar (o producto punto).
La condición para la adición y el producto escalar es que se tienen que hacer entre n-tuplas del mismo conjunto R^n, es decir con el mismo número de componentes.
Por ponerlo de alguna forma son como perros, gatos, hamsters, uno no puede cruzarlos.
Bueno, para realizar la adición simplemente se suma componente por componente de cada n-tupla, es decir, el primer componente de la primera n-tupla, con el primero de la segunda n-tupla, el segundo con el segundo y el resultado debe dar otra n-tupla.
Las propiedades de la adición son las siguientes:
1. (a+b)+c = a+(b+c) (asociativa).
2. Existe o =(0,...,0), tal que para todo a, a+o=a.
Es decir que o es una n-tupla nula y es el módulo bajo la operación de adición.
3. Para todo a = (a_1, a_2,...,a_n), existe una n-tupla designada -a = (-a_1, -a_2,...,-a_n) con la propiedad de que a + (-a) = o = (0,...,0).
El término -a se lee inverso aditivo de a (invertida.
4. a+b = b+a (conmutativa).
El producto de un número real (escalar) por una n-tupla es multiplicar cada uno de los componentes de la n-tupla por el escalar.
ej. 2a = (2a_1, 2a_2, ... , 2a_n)
Estos también son conocidos como conjuntos de n-tuplas, donde una n-tupla son varios elementos ordenados:
R^n = {(a_1, a_2,...,a_n)/tal que a_i está en R (conjunto de los reales), para todo i=1,...,n
Algunos de estos conjuntos son muy conocidos, por ejemplo el de las parejas ordenadas
R^2 = {(a_1,a_2)/a_1,a_2 en R}
Este tiene su representación como puntos en el plano cartesiano.
R^3 tiene su representación como puntos en un espacio tridimensional. Otros conjuntos R^n con n > 3 son también usados pero no tienen representación geométrica.
Recordemos que un elemento es una n-tupla (a_1,a_2,...,a_n), a su vez cada n-tupla tiene componentes que son a_1, a_2, etc. que para el curso son números reales).
Con los elementos de estos conjuntos podemos hacer algunas operaciones: la adición, el producto de un número real por una n-tupla y el producto escalar (o producto punto).
La condición para la adición y el producto escalar es que se tienen que hacer entre n-tuplas del mismo conjunto R^n, es decir con el mismo número de componentes.
Por ponerlo de alguna forma son como perros, gatos, hamsters, uno no puede cruzarlos.
Bueno, para realizar la adición simplemente se suma componente por componente de cada n-tupla, es decir, el primer componente de la primera n-tupla, con el primero de la segunda n-tupla, el segundo con el segundo y el resultado debe dar otra n-tupla.
Las propiedades de la adición son las siguientes:
1. (a+b)+c = a+(b+c) (asociativa).
2. Existe o =(0,...,0), tal que para todo a, a+o=a.
Es decir que o es una n-tupla nula y es el módulo bajo la operación de adición.
3. Para todo a = (a_1, a_2,...,a_n), existe una n-tupla designada -a = (-a_1, -a_2,...,-a_n) con la propiedad de que a + (-a) = o = (0,...,0).
El término -a se lee inverso aditivo de a (invertida.
4. a+b = b+a (conmutativa).
El producto de un número real (escalar) por una n-tupla es multiplicar cada uno de los componentes de la n-tupla por el escalar.
ej. 2a = (2a_1, 2a_2, ... , 2a_n)
domingo, 10 de octubre de 2010
Los números naturales y los enteros
Ahora empecemos a llenar la recta de los reales, pero comencemos por los números más sencillos: los naturales.
1, 2, 3, ...
Estos son los que nos sirven para contar, se les llama naturales porque fueron los primeros que utilizó el ser humano.
Sin embargo, que pasa cuando no hay nada que contar, para eso inventamos el 0 y así tenemos los siguientes números:
0, 1, 2, 3, ...
Con ellos podemos hacer operaciones básicas, como la suma, la resta, hasta multiplicarlos y dividirlos, pero, ¿qué pasa cuando nos encontramos con expresiones como 5-7?
Entonces necesitamos un conjunto más, el de los negativos (también llamado de los no-positivos):
..., -3, -2, -1
Y así completamos a los enteros:
..., -3, -2, -1, 0, 1, 2, 3, ...
Ahora en nuestra querida recta los podemos representar de la siguiente manera:
Escogemos un punto arbitrariamente y a ese lo designamos el origen, al cual le asignamos el valor de 0, por convención a la derecha de este punto ubicaremos los números positivos y a su izquierda los negativos.

Luego escogemos arbitrariamente una unidad de distancia. Cada número natural n lo representaremos como el punto que se encuentra a una distancia de n unidades del origen.
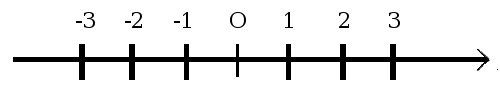
Pero todavía estamos muy lejos de la recta real, pues si sólo dejamos los puntos de los naturales la veríamos así:
. . . . . . . . . . . . . . .
Si luego dividimos cada unidad en unidades más pequeñas encontraremos los números racionales o fraccionarios: 1/2, 3/4, 1/3, etc. los cuales también podemos representar como decimales finitos o periódicos: 0,5; 0,75; 0,333...; etc.
Podemos dividir nuestras unidades en fracciones muy pequeñas (por ej. 1/1573), con lo cual podríamos llenar cada vez más nuestra recta y ya se vería como una recta.
___________________________________________________
Pero si nos acercamos veríamos puntos separados:
.........................................................................................................
Pues todavía nos falta definir a los números irracionales para completar a los reales, lo cual haremos en una próxima entrada, por ahora vamos con algo de música, esta vez un tema clásico de una excelente película.
Saludos.
1, 2, 3, ...
Estos son los que nos sirven para contar, se les llama naturales porque fueron los primeros que utilizó el ser humano.
Sin embargo, que pasa cuando no hay nada que contar, para eso inventamos el 0 y así tenemos los siguientes números:
0, 1, 2, 3, ...
Con ellos podemos hacer operaciones básicas, como la suma, la resta, hasta multiplicarlos y dividirlos, pero, ¿qué pasa cuando nos encontramos con expresiones como 5-7?
Entonces necesitamos un conjunto más, el de los negativos (también llamado de los no-positivos):
..., -3, -2, -1
Y así completamos a los enteros:
..., -3, -2, -1, 0, 1, 2, 3, ...
Ahora en nuestra querida recta los podemos representar de la siguiente manera:
Escogemos un punto arbitrariamente y a ese lo designamos el origen, al cual le asignamos el valor de 0, por convención a la derecha de este punto ubicaremos los números positivos y a su izquierda los negativos.

Luego escogemos arbitrariamente una unidad de distancia. Cada número natural n lo representaremos como el punto que se encuentra a una distancia de n unidades del origen.
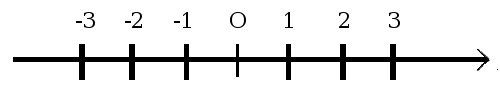
Pero todavía estamos muy lejos de la recta real, pues si sólo dejamos los puntos de los naturales la veríamos así:
. . . . . . . . . . . . . . .
Si luego dividimos cada unidad en unidades más pequeñas encontraremos los números racionales o fraccionarios: 1/2, 3/4, 1/3, etc. los cuales también podemos representar como decimales finitos o periódicos: 0,5; 0,75; 0,333...; etc.
Podemos dividir nuestras unidades en fracciones muy pequeñas (por ej. 1/1573), con lo cual podríamos llenar cada vez más nuestra recta y ya se vería como una recta.
___________________________________________________
Pero si nos acercamos veríamos puntos separados:
.........................................................................................................
Pues todavía nos falta definir a los números irracionales para completar a los reales, lo cual haremos en una próxima entrada, por ahora vamos con algo de música, esta vez un tema clásico de una excelente película.
Saludos.
viernes, 8 de octubre de 2010
La linea, aquel infinito conjunto de puntos
Para empezar con las entradas de matemática vamos a empezar con el concepto con el que empiezan casi todos los libros de pre-cálculo: conjuntos.
Pero antes de eso quisiera que recordáramos otro concepto que tal vez nos ayude a entender un poco mejor el concepto de los números reales:
La linea recta, la cual es una sucesión infinita de puntos en una sola dimensión.
_______________________________________________________________
Bueno, si está compuesta por puntos si hacemos un zoom lo lo suficientemente grande deberíamos ver los puntos, como cuando en un programa de manipulación le hacemos zoom a la imagen y empezamos a ver los píxeles, ¿no?
.............................................................................................................................................
Pues no, en teoría por más que nos acerquemos si alcanzamos a ver la recta no la veríamos siquiera aumentar de tamaño, pues está solo tiene una dimensión, además como contiene infinitos puntos, entre dos puntos, por más cercanos que se encuentren siempre habrá infinitos puntos.
_______________________________________________________________
Bueno, esta linea recta pronto nos servirá para representar a los números reales, pues como dijimos una linea tiene infinitos puntos, así como hay infinitos números. Poquito a poco la iremos llenando.
Y para terminar una entretenida historia.
Pero antes de eso quisiera que recordáramos otro concepto que tal vez nos ayude a entender un poco mejor el concepto de los números reales:
La linea recta, la cual es una sucesión infinita de puntos en una sola dimensión.
_______________________________________________________________
Bueno, si está compuesta por puntos si hacemos un zoom lo lo suficientemente grande deberíamos ver los puntos, como cuando en un programa de manipulación le hacemos zoom a la imagen y empezamos a ver los píxeles, ¿no?
.............................................................................................................................................
Pues no, en teoría por más que nos acerquemos si alcanzamos a ver la recta no la veríamos siquiera aumentar de tamaño, pues está solo tiene una dimensión, además como contiene infinitos puntos, entre dos puntos, por más cercanos que se encuentren siempre habrá infinitos puntos.
_______________________________________________________________
Bueno, esta linea recta pronto nos servirá para representar a los números reales, pues como dijimos una linea tiene infinitos puntos, así como hay infinitos números. Poquito a poco la iremos llenando.
Y para terminar una entretenida historia.
Bienvenida
Bueno, primero que todo bienvenidos a este blog en el que quiero publicar mis descubrimientos diarios en este viaje por la matemática que empezará con las matemáticas previas al cálculo como un repaso antes de iniciar mis estudios en la universidad.
Para empezar me gustaría dar un poco de la bibliografía que estaré utilizando por si alguien quiere averiguar un poco más por su cuenta. Entre los libros que más estaré consultando están los siguientes:
Algébra de Baldor
Precálculo de Stewart
Matemáticas previas al cálculo de Leithold
Álgebra y trigonometría de Swokowski
No los utilizo porque sean los mejores, si no porque los tengo más a la mano y son de los que más entiendo, hay muchos otros libros sobre estos temas y con dedicación cualquiera es bueno, aparte del obvio recurso de la internet.
Y para completar el título del blog aquí un video de una versión de Bach
Para empezar me gustaría dar un poco de la bibliografía que estaré utilizando por si alguien quiere averiguar un poco más por su cuenta. Entre los libros que más estaré consultando están los siguientes:
Algébra de Baldor
Precálculo de Stewart
Matemáticas previas al cálculo de Leithold
Álgebra y trigonometría de Swokowski
No los utilizo porque sean los mejores, si no porque los tengo más a la mano y son de los que más entiendo, hay muchos otros libros sobre estos temas y con dedicación cualquiera es bueno, aparte del obvio recurso de la internet.
Y para completar el título del blog aquí un video de una versión de Bach
Suscribirse a:
Entradas (Atom)