Los números naturales y los enteros

Ahora empecemos a llenar la recta de los reales, pero comencemos por los números más sencillos: los naturales.

1, 2, 3, ...

Estos son los que nos sirven para contar, se les llama naturales porque fueron los primeros que utilizó el ser humano.

Sin embargo, que pasa cuando no hay nada que contar, para eso inventamos el 0 y así tenemos los siguientes números:

0, 1, 2, 3, ...

Con ellos podemos hacer operaciones básicas, como la suma, la resta, hasta multiplicarlos y dividirlos, pero, ¿qué pasa cuando nos encontramos con expresiones como 5-7?

Entonces necesitamos un conjunto más, el de los negativos (también llamado de los no-positivos):

..., -3, -2, -1

Y así completamos a los enteros:

..., -3, -2, -1, 0, 1, 2, 3, ...

Ahora en nuestra querida recta los podemos representar de la siguiente manera:

Escogemos un punto arbitrariamente y a ese lo designamos el origen, al cual le asignamos el valor de 0, por convención a la derecha de este punto ubicaremos los números positivos y a su izquierda los negativos.



Luego escogemos arbitrariamente una unidad de distancia. Cada número natural n lo representaremos como el punto que se encuentra a una distancia de n unidades del origen.



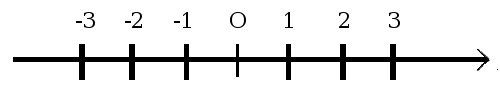
Pero todavía estamos muy lejos de la recta real, pues si sólo dejamos los puntos de los naturales la veríamos así:

. . . . . . . . . . . . . . .

Si luego dividimos cada unidad en unidades más pequeñas encontraremos los números racionales o fraccionarios: 1/2, 3/4, 1/3, etc. los cuales también podemos representar como decimales finitos o periódicos: 0,5; 0,75; 0,333...; etc.

Podemos dividir nuestras unidades en fracciones muy pequeñas (por ej. 1/1573), con lo cual podríamos llenar cada vez más nuestra recta y ya se vería como una recta.

___________________________________________________

Pero si nos acercamos veríamos puntos separados:
.........................................................................................................
Pues todavía nos falta definir a los números irracionales para completar a los reales, lo cual haremos en una próxima entrada, por ahora vamos con algo de música, esta vez un tema clásico de una excelente película.



Saludos.